1. 1. Contribution
2. 2. Optic Flow? (为什么定义都会下错啊？)
3. 3. Approach
   1. 3.1 Correaltion Pyramid and Computation
   2. 3.2 Iterative Updates
   3. 3.3 Loss Function
4. 4. Experiment
5. 4.1 Ablation

1. Contribution

1. RAFT maintains and updates a single fixed flow field at high resolution.
2. The update operator of RAFT is recurrent and lightweight
3. The update operator consists of a convolutional GRU that performs lookups on 4D multi-scale correlation volumes (DualRefine’s reference)

2. Optic Flow? (为什么定义都会下错啊？)

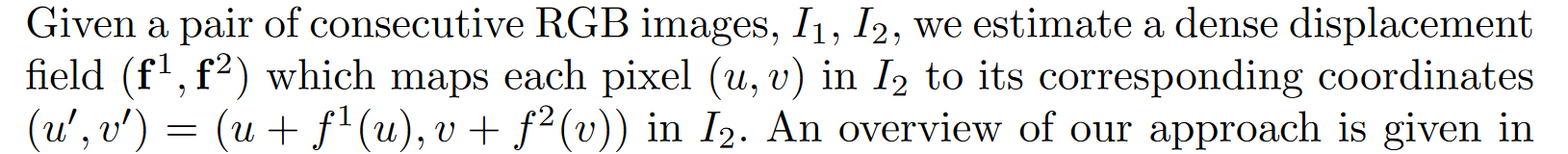
3. Approach

3.1 Correaltion Pyramid and Computation

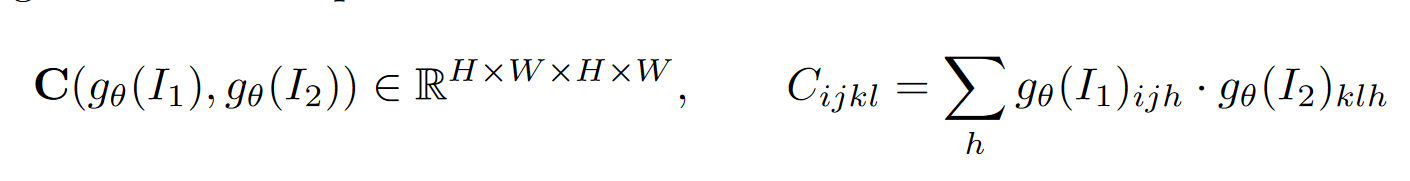
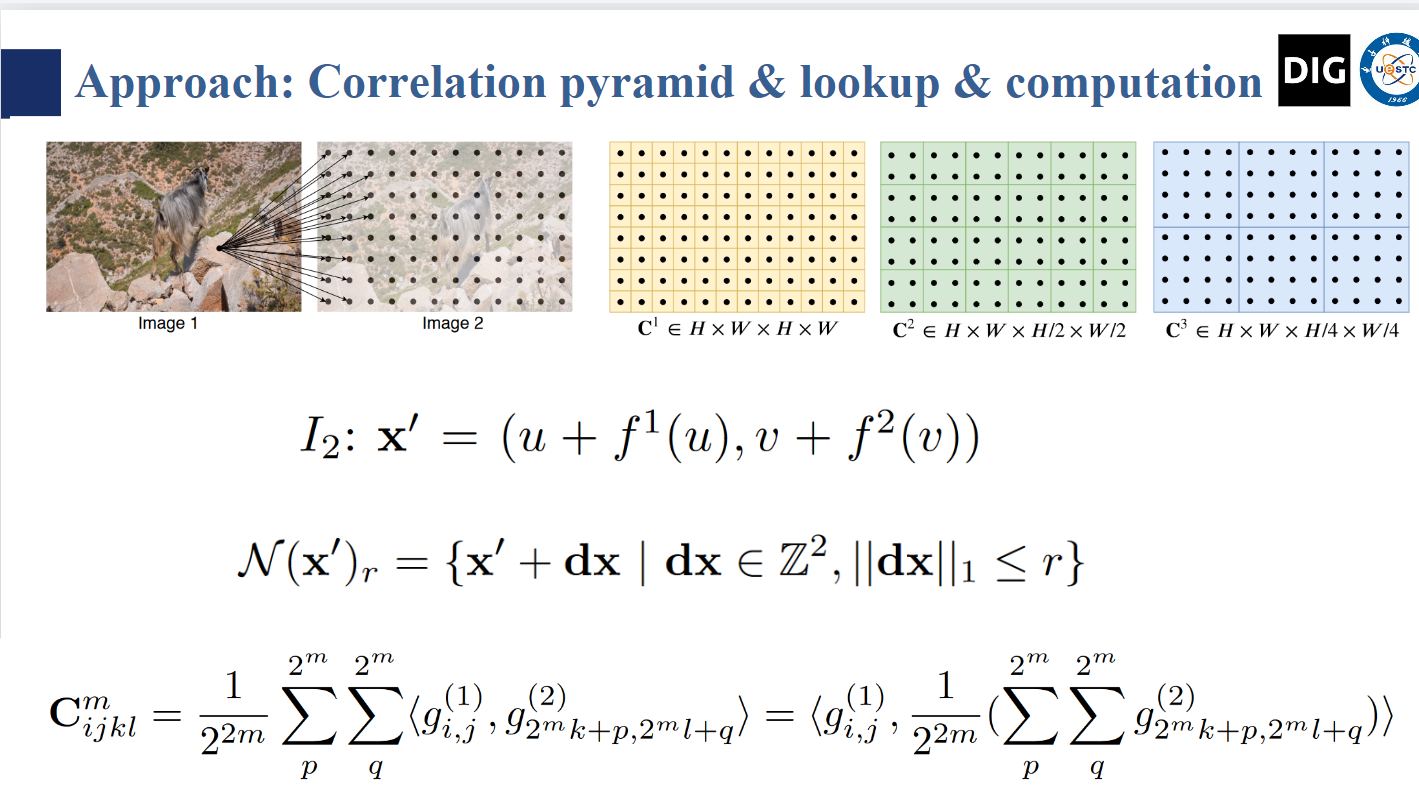
1. 我们保持了高分辨率信息(C^1, C^2)，使我们的方法能够恢复快速移动的小物体的运动。C^n通过平均池化来构建的。

2. 邻域上的点是I_1上的点到I_2上的潜在位置，在迭代计算的过程中，需要计算X和领域内点的相关性，可以直接查询出来。（双线性采样）

3. 我们在金字塔的所有层级上进行查找，这样层级 k 的相关卷 Ck 就可以使用网格 N (x′/2^k)r 进行索引。各层次的半径恒定意味着较低层次的上下文更大：对于最低层 k = 4，半径为 4 相当于原始分辨率下 256 （确定不是一个像素先对应了高分辨率的64个，然后再乘以16=1024？）个像素的范围。然后将各层次的值串联成一张特征图。如此一来， 在越低分辨率的 correlation 矩阵上 lookup 到的结果，其在语义层面上包含的 receptive field 越广。

4. 用内积的线性和平均池化，实现 O(NM) 的时间复杂度。实际上计算的是 g1 和 m 次平均池化下采样后的内积（先计算高分辨率然后平均池化 correlation 和 先池化 feature 后计算）。我们不预先计算相关性，而是预先计算池化的的图像特征图。在每次迭代中，我们只在需要查找时计算每个相关值。这样的复杂度为 O(NM)？
   由于 GPU 上的矩阵例程经过了高度优化，因此预计算所有配对很容易实现。（😄）

   Github: this implementation is somewhat slower than all-pairs, but uses significantly less GPU memory during the forward pass.

3.2 Iterative Updates

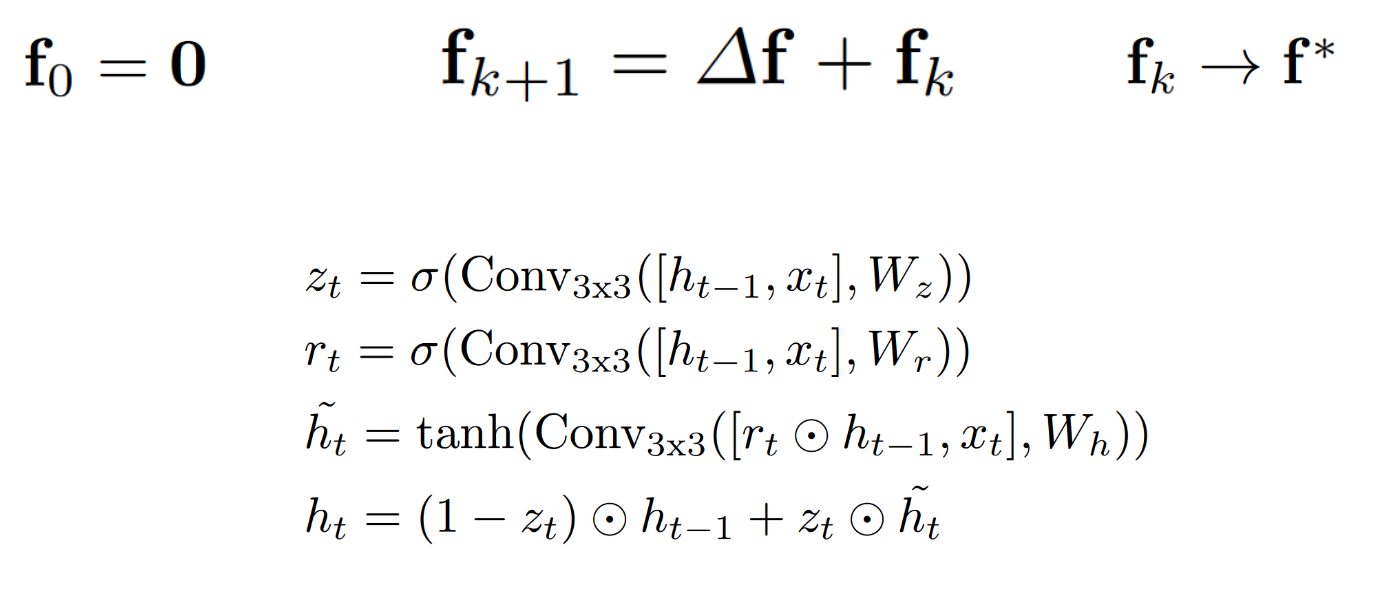
论文中关于 的表述不如看图，给定当前流量估计值 后，我们将利用该估计值从相关金字塔中提取相关特征，如 3.2 节所述。然后由 2 个卷积层对相关特征进行处理。此外，我们将 2 个卷积层应用于光流估计本身，以生成流量特征。最后，我们直接注入上下文网络的输入。 就是相关特征（每层的lookup concatenated）、流量特征和上下文特征的集合。

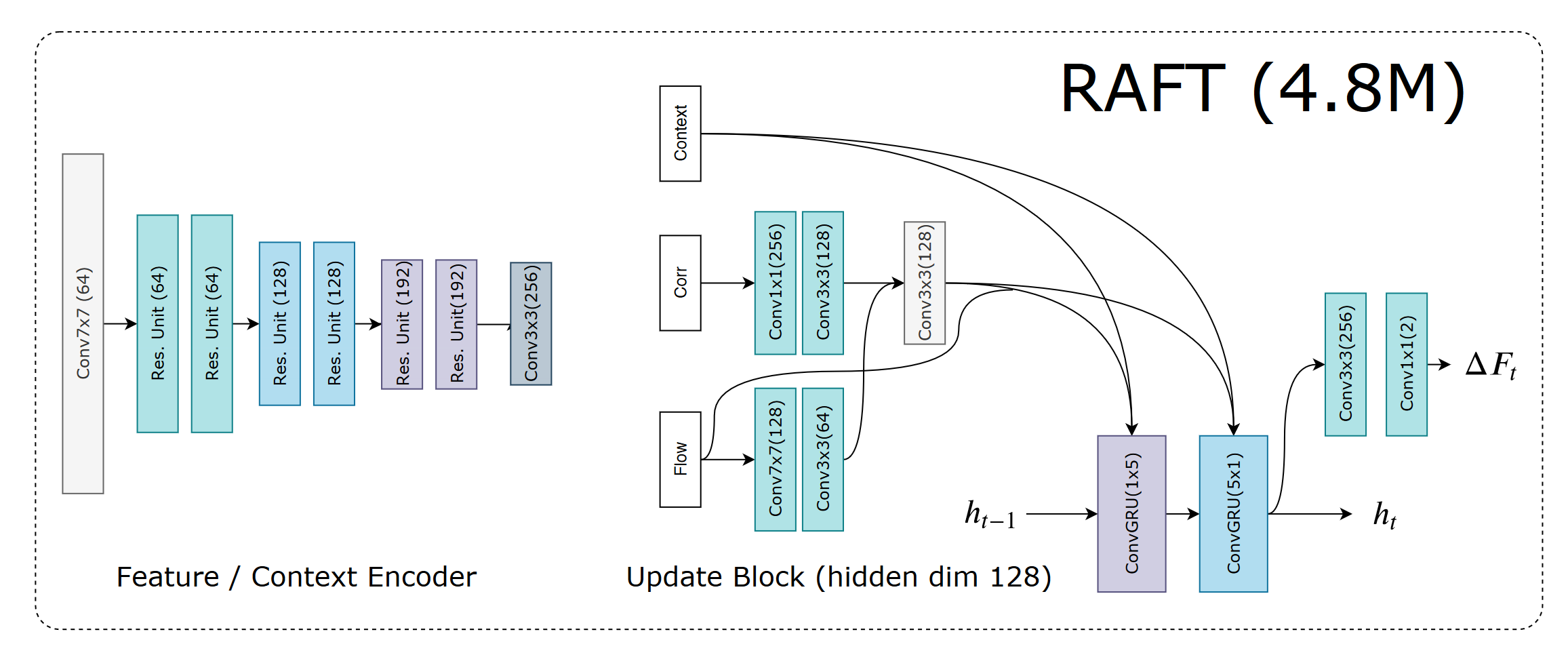
3.3 Loss Function

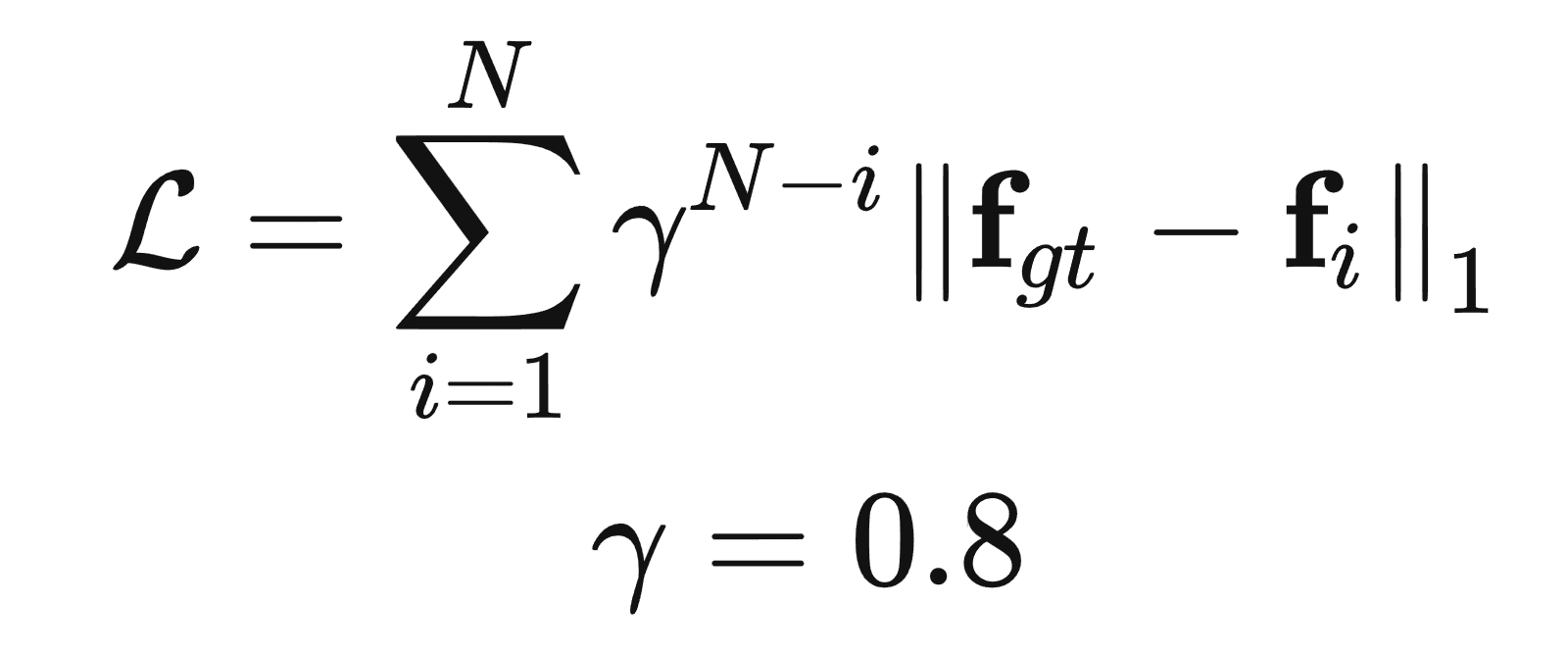
迭代前期的权重比较低。

4. Experiment

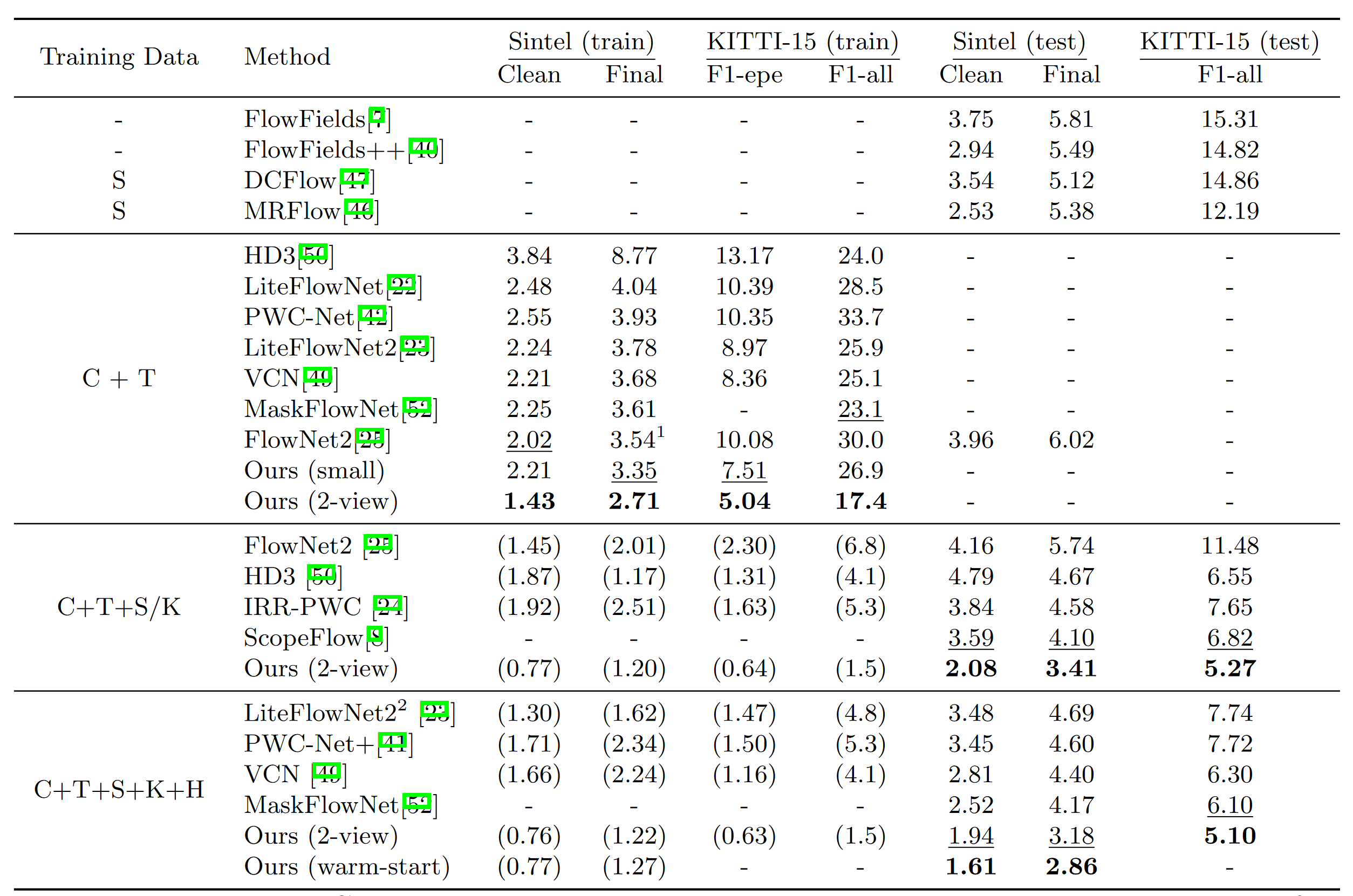
4.1 Ablation

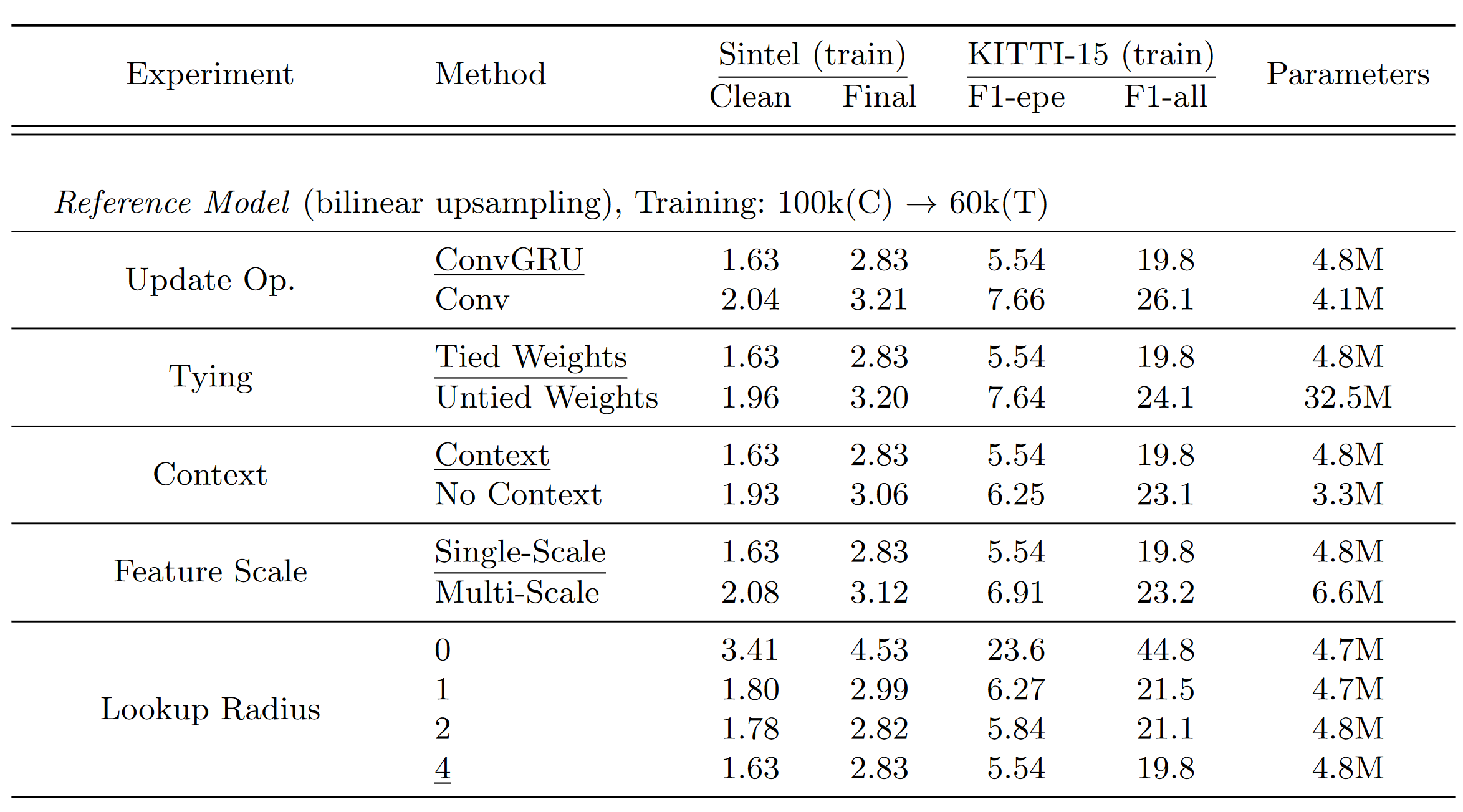
• Feature Scale：是否基于多个 scale 的 feature去构造 Correlation Pyramid 而不是平均池化。
• Tied Weights:

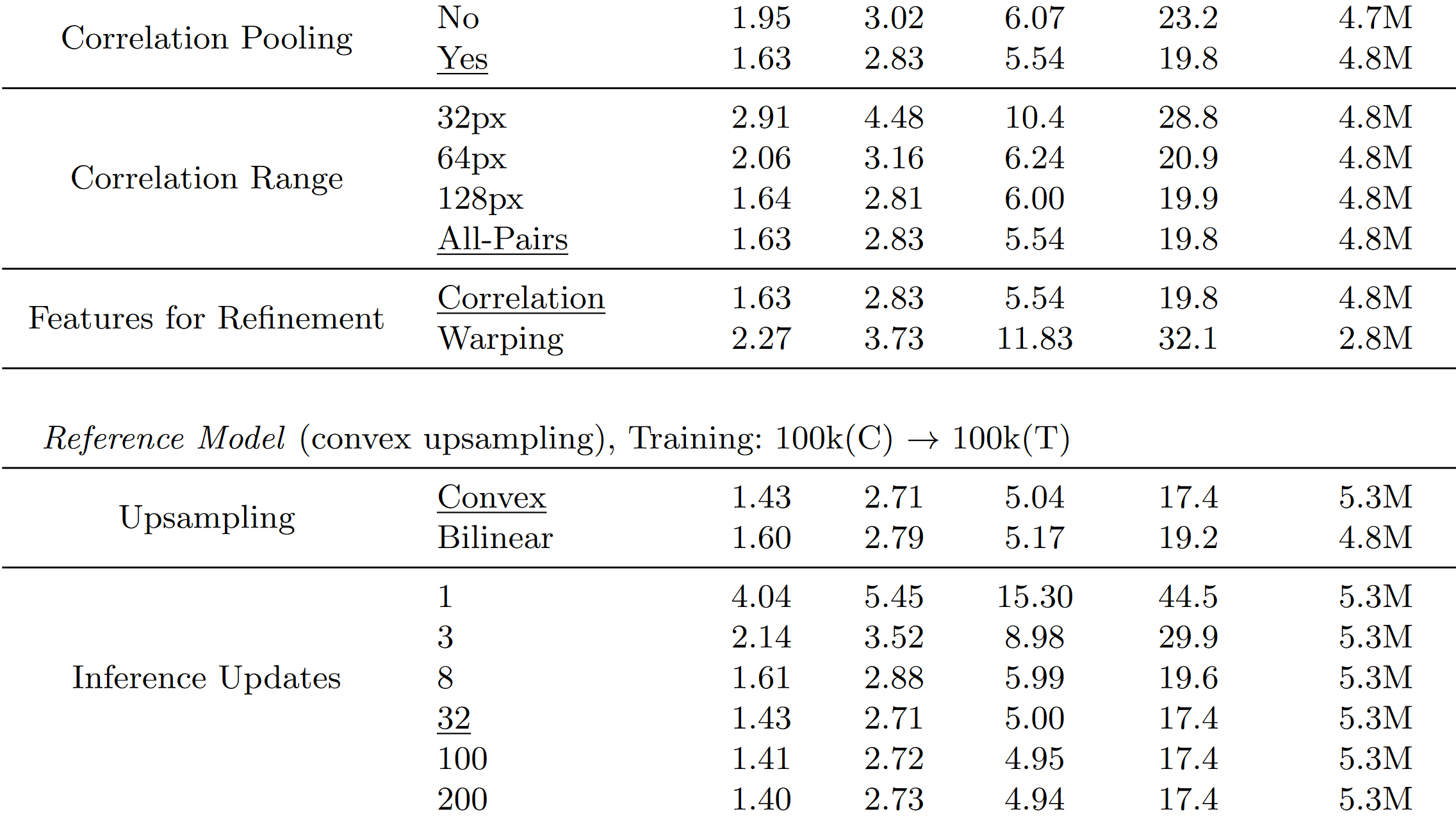
• Features for refinement：使用当前的光流估计值将 I2 中的特征 warp 到 I1 上，然后根据residual来优化（自监督深度估计是吧）。
• convex upsampling:
• Inference updates: 推理的时候多推理不会发散，很快就收敛了。